Решил я как-то проверить закон Ома. Применительно к лампе накаливания. Измерил сопротивление лампочки Лисма 230 В 60 Вт, оно оказалось равным 59 Ом. Я было удивился, но потом вспомнил слово, которое всё объясняло – бареттер.
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если это бы был не вольфрам, а обычный резистор, его рассеиваемая мощность при напряжении 230 Вольт была бы P = U2/R = 896. Почти 900 Ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при подключении датчиков.
Как же измерить рабочее сопротивление нити лампы накаливания? А никак. Его можно только определить косвенным путем, из закона знаменитого Ома. (Строго говоря, все омметры используют тот же закон – прикладывают напряжение и меряют ток). И мультиметром тут не обойдешься.
Используя косвенный метод и лампочку Лисма 24 В с мощностью 40 Вт, я составил вот такую табличку:
Содержание статьи:
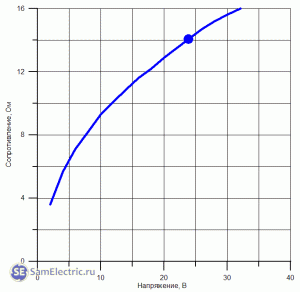
Зависимость сопротивления нити лампы накаливания от напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| % напряжения | 8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Ток | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
(продолжение таблицы)
| Напряжение | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| % напряжения | 75.0 | 83.3 | 91.7 | 100.0 | 108.3 | 116.7 | 125.0 | 133.3 |
| Ток | 1.47 | 1.55 | 1.63 | 1.7 | 1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 | 14.1 | 14.7 | 15.2 | 15.6 | 16.0 |
| Мощность | 26.46 | 31 | 35.86 | 40.8 | 46.02 | 51.52 | 57.6 | 64 |
(Номинальные параметры выделены)
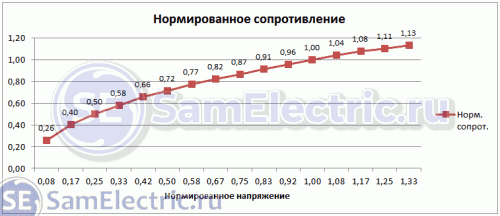
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейная. Это может проиллюстрировать график, приведенный ниже. Рабочая точка на графике выделена.
Кстати, сопротивление подопытной лампочки, измеренное с помощью цифрового мультиметра – около 1 Ома. Предел измерения – 200 Ом, при этом выходное напряжение вольтметра – 0,5 В. Эти данные также укладываются в полученные ранее.
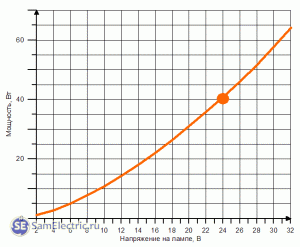
Зависимость мощности от напряжения:
Для ламп на напряжение 230 В на основании экспериментальных данных была составлена вот такая табличка:
| Мощность лампочки, Вт | 25 | 40 | 60 | 75 | 100 |
| R холодной нити,Ом | 150 | 90-100 | 60-65 | 45-50 | 37-40 |
| R горячей нити, Ом | 1930 | 1200 | 805 | 650 | 490 |
| Rгор./Rхол. | 12 | 12 | 13 | 13 | 12 |
Из этой таблицы видно, что сопротивление нити лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. А это значит, что во столько же раз увеличивается потребляемая мощность в первоначальный момент.
Стоит отметить, что сопротивление в холодном состоянии измерялось мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же укладывается в идею статьи.
“Горячее” сопротивление измерялось косвенным методом.
UPD: Сопротивление нити накаливания люминесцентных ламп
Дополнение к статье, чтобы получился ещё более полный материал.
Лампы с цоколем Т8, сопротивление спирали в зависимости от мощности :
10 Вт – 8,0…8,2 Ом
15 Вт – 3,3…3,5 Ом
18 Вт – 2,7…2,8 Ом
36 Вт – 2,5 Ом.
Сопротивление измерялось цифровым омметром на пределе 200 Ом.
Формула мощности и напряжения
Обновление статьи от января 2018. У меня на блоге появилась статья автора Станислава Матросова, который развил тему сопротивления спирали лампочки с теоретической стороны. Он вывел формулу, согласно которой:
Для любой лампы накаливания существует параметр, стабильный в широком диапазоне электрических режимов. Этим параметром является отношение куба напряжения к квадрату мощности:
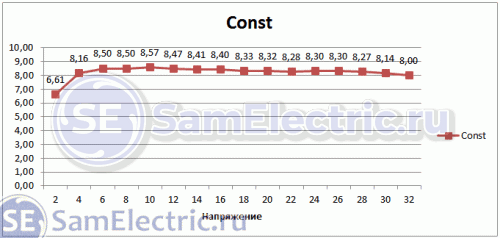
Я решил на основе данных, полученных в статье, посчитать эту величину в Экселе. Вот что у меня получилось:
| U | P | U^3 | P^2 | Const |
| 2 | 1,1 | 8 | 1,21 | 6,61157 |
| 4 | 2,8 | 64 | 7,84 | 8,163265 |
| 6 | 5,04 | 216 | 25,4016 | 8,503401 |
| 8 | 7,76 | 512 | 60,2176 | 8,502498 |
| 10 | 10,8 | 1000 | 116,64 | 8,573388 |
| 12 | 14,28 | 1728 | 203,9184 | 8,473978 |
| 14 | 18,06 | 2744 | 326,1636 | 8,412956 |
| 16 | 22,08 | 4096 | 487,5264 | 8,401596 |
| 18 | 26,46 | 5832 | 700,1316 | 8,329863 |
| 20 | 31 | 8000 | 961 | 8,324662 |
| 22 | 35,86 | 10648 | 1285,94 | 8,280327 |
| 24 | 40,8 | 13824 | 1664,64 | 8,304498 |
| 26 | 46,02 | 17576 | 2117,84 | 8,29902 |
| 28 | 51,52 | 21952 | 2654,31 | 8,270321 |
| 30 | 57,6 | 27000 | 3317,76 | 8,138021 |
| 32 | 64 | 32768 | 4096 | 8 |
Действительно, константа, которая с некоторой погрешностью во всём диапазоне равна 8,2±0,2. Её размерность – “Вольт в кубе на Ватт в квадрате”.
Низкое значение константы в начале диапазона объяснено автором в приведенной по ссылке статье.
Теперь, зная значение этой константы (8,2), можем записать формулу зависимости мощности от напряжения лампочки накаливания 40Вт 24В:
Формула для сопротивления
Но вернёмся к теме статьи. Проверим вывод Станислава Матросова о том, что сопротивление лампочки пропорционально корню из напряжения. Из предыдущих выводов можно вывести формулу для конкретной лампочки 40Вт 24В:
Теперь проверим, как эта формула соотносится с полученными мною экспериментальным данным (см. таблицу в начале статьи). Составим такую таблицу:
| 1. Напря- жение, В | 2. Норм. напр. | 3. Сопрот., Ом | 4. Норм. сопрот. | 5. Корень из норм. напряж. | 6. Корень из напряж. Х Корень из Const |
| 2 | 0,08 | 3,6 | 0,26 | 0,29 | 4,04 |
| 4 | 0,17 | 5,7 | 0,40 | 0,41 | 5,72 |
| 6 | 0,25 | 7,1 | 0,50 | 0,50 | 7,01 |
| 8 | 0,33 | 8,2 | 0,58 | 0,58 | 8,09 |
| 10 | 0,42 | 9,3 | 0,66 | 0,65 | 9,04 |
| 12 | 0,50 | 10,1 | 0,72 | 0,71 | 9,91 |
| 14 | 0,58 | 10,9 | 0,77 | 0,76 | 10,70 |
| 16 | 0,67 | 11,6 | 0,82 | 0,82 | 11,44 |
| 18 | 0,75 | 12,2 | 0,87 | 0,87 | 12,13 |
| 20 | 0,83 | 12,9 | 0,91 | 0,91 | 12,79 |
| 22 | 0,92 | 13,5 | 0,96 | 0,96 | 13,41 |
| 24 | 1,00 | 14,1 | 1,00 | 1,00 | 14,01 |
| 26 | 1,08 | 14,7 | 1,04 | 1,04 | 14,58 |
| 28 | 1,17 | 15,2 | 1,08 | 1,08 | 15,13 |
| 30 | 1,25 | 15,6 | 1,11 | 1,12 | 15,66 |
| 32 | 1,33 | 16 | 1,13 | 1,15 | 16,18 |
Таблица требует пояснений. Чтобы была соблюдена размерность, я нормировал экспериментально заданное напряжение (столбец 2) и рассчитанное сопротивление (столбец 4).
Колонка 5 – это корень из нормированного напряжения, и видно, что значения этой колонки отлично совпадают с колонкой 4!
Но давайте вернемся в реальному сопротивлению, и рассчитаем его по приведенной выше формуле (Зависимость сопротивления от напряжения). Это – 6-я колонка. Хорошо видно, что расчет по формуле практически идеально совпадает с расчетом из экспериментальных данных!
Кто хочет проверить мои расчеты, прикладываю файл: • Файл с расчетами и графиками / Файл с расчетами и графиками к статье про лампу накаливания, xlsx, 19.51 kB, скачан: 1458 раз./
Всё, учебник физики можно переписывать! ;)
Кому интересно – задачка про последовательное подключение двух лампочек.

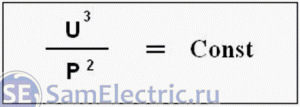
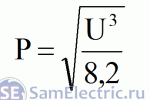
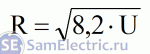
















(Строго говоря, все омметры используют тот же закон — прикладывают напряжение и меряют ток)
Открою вам секрет – они меряют тоже напряжение, только которое падает на шунте.
Сергей, спасибо за уточнение! Действительно, как нам написал на доске преподаватель Теории Цепей: “Амперметров НЕТ!”.
Ведь любой амперметр – это фактически вольтметр, которой измеряет напряжение на шунте, который включается в разрыв измеряемой цепи.
а любой вольтметр есть микроамперметр , ибо без течки тока нечем стрелку отклонять…
Скажите это электромагнитному амперметру состоящему из одной катушки из толстого провода и работающего в паре с трансформатором тока.
У вас неточные замеры вы считаете напряжение и сопртивление нити спирали а куда девали нагрев лампы при нагревании сопротивление падает а вы этого не учитываете поэтому расчеты неточные
А давайте обсудим жучка из меди на 250 ампер-400 в.?
При нагревании сопротивление нити накала увеличивается.
Спасибо за краткое изложение статьи)))
Самое худшее когда момент включения лампочки приходится на пик синусоиды.
Точно. Возьмём максимальный критический случай. Нормальные пределы напряжения – 220+-10%, то есть максимум 242В. Пиковое значение напряжения – 242*1,41=341В !!!
Теперь рассмотрим лампочку на 100 Вт, у неё сопротивление холодной нити 40 Ом. Мощность P=UI=UU/R= 2910 Ватт!
То есть, лампа 100 Вт в момент включения может потреблять мгновенную мощность до 3 кВт, и это не авария, а штатный режим!
Тяжело иногда приходится лампочке!
А как Вы думаете какое сопротивление холодной нити будет у лампочки на 300Вт и на 500Вт?
Т.е. порядка 13А будет ток в первые 2-3мс. Верно?
Да это не мудрено что сопротивление растет мо мере нагревания электроны то движуться крез кристалческие решетки а при нагревании начинают быстрее двигаться и ударяться отталкиваясь друг от друга. Ну и по закону сохранения энергии кинктическая переходит в тепловую както так.
Интересная таблица я заметил что между 18 и 24 ток и мощость практически не меняесться а вот как бы узнать яркость лампы понятно что она изменяетсья не линейно то есть уменьшение мощности на 20% приведет к удельному изменению якрсти скажем на 40. Ну вот найти если оптимальный режим работы лампы скажем 70% яркости и подходящее напряжение тогда она будет гореть долго но тускло. Хотя перегорают лампы накаливания именно изза высокого тока в момент включения.
Как говорил наш преподаватель, перегорают лампы не из-за высокого тока в момент включения, а из-за синусоиды, а именно из-за высокой амплитуды колебания тока. Если к примеру синусоиду срезать наполовину диодом, то лампа будет мерцать, но срок её службы будет увеличен многократно.
Согласен. В течение периода амплитуда напряжения на лампочке (мгновенное значение напряжения) изменяется от 0 до 220х1,41=310 В.
Вопрос, в какой момент это напряжение будет приложено к лампочке.
Вообще-то, как мне кажется, диод убирает одну половину периода гармоники. В итоге получается не совсем то, о чем вы пишите.
а вы когда нибудь разбирали вольтметр? попробуйте и увидите что он по сути своей есть амперметр. в вольтметре фазу и ноль соединяет неразрывный проводник в котором из-за свойства материала (сопротивление току) ограничивается ток до малого (а иначе явное КЗ)и участок этого проводника свит в спираль для создание поля, которое отклоняет стрелку прибора. так что “отсутствуют..” не амперметры а вольтметры.
Вольтметр суть микроамперметр последовательно с резистором высокого сопротивления.
А любой амперметр – это вольтметр, измеряющий напряжение на калиброванном шунте.
Подробнее – в статье про устройство счетчика.
А Вы когда-нибудь разбирали амперметры? Это прибор, который фактически измеряет напряжение на шунте, входящем в его состав.
И вольтметр, и амперметр созданы на основе микроамперметра. А это- рамка с катушкой (электромагнит) в поле постоянного магнита. Магниты, взаимодействуя, отклоняют рамку со стрелкой.
вообщето это моя работа… конструкции есть разные, наиболее простую я описал (вольтметр внутри это амперметр плюс катушка сопротивления и проводник более тонкий и все), и там нет шунтов и они не нужны. описанная вами конструкция тоже есть, но это уже видоизменение базовой.
А, тогда понятно… Я с такими как описывал дела не имел давно, ещё в студенческую пору)
А суть высказывания в том, что амперметр имеет сопротивление (хоть и малое), и вносит изменение в режим работы схемы, поэтому ток вычисляют косвенно, по закону Ома.
Не затруднит ли вас нанести еще и температуру нити (вольфрамовой)по точкам ваших графиков?(или из расчетов по готовым таблицам или при возможности доступа к подходящим термометрам).
Задумал использовать смн лампочку(возможны и еще варианты) в роли термометра сопротивления, точность в пределах нескольких градусов(в промышленности идет в основном платина, но там свои требования к точности и стабильности). Хотел прикинуть величину сопротивления в нужном мне диапазоне (примерно до 400 по Цельсию).
Смущают немного еще контакты в держателях нити(стабильность их и термоэлектрические эффекты) и устойчивость колбы к перепаду температуры(возможно резкое охлаждение при попадании воды). Кварцевые колбы только в слишком мощных лампах встречались. Привлекает относительная доступность лампочек.
Да я бы нанёс, но не знаю, как её измерить…
Лампочка в качестве датчика – не слишком ли громоздко? Есть термопары, не намного дороже лампочки. Недавно покупал для терморегулятора. Оказалось, термопары продаются в радиотоварах по 50 руб как ЗИП для мультиметров.
а если термистор поставить последовательно с лампой, только его рядом с ней чтобы он нагревался, у него сопротивление уменьшается от нагрева , например NTC 5D-15,NTC 10D-15,NTC 10D-9 и т.д. .
Для любой лампочки отношение куба напряжения к квадрату мощности – есть величина постоянная.
Методика использования формулы проста до примитивности.
Берем лампочку, читаем на колбе или на цоколе параметры, на которые она рассчитана – напряжение и мощность, рассчитываем константу, потом вставляем в формулу любое произвольное напряжение и вычисляем мощность, которая выделится на лампочке.
Зная мощность несложно вычислить ток.
Зная ток несложно вычислить сопротивление нити накаливания.
https://www.proza.ru/2016/09/19/1858
..
Я эту формулу вывел лет 20 назад и пользуюсь постоянно.
Никаких фокусов не наблюдалось.
Можно проверить данные таблиц. все совпадает “пуля в пулю”
Спасибо! За формулу и отличную статью!
Там есть еще одна статья.
Она несколько неудачно оформлена, потому что возможности того сайта не позволяют внедрить в тело статьи несколько рисунков. Только один рисунок.
Потому то я на одном рисунке сгрудил все формулы… Ну и тело статьи получилось очень туманное.
Там я описываю опыт который проводил соединив схему из трех лампочек “две параллельно и еще одна последовательно” и комбинировал различные сочетания… То 95 ватт последовательно, а 40 и 60 параллельно, то 40 последовательно а 60 и 95 параллельно…
По всякому перекоммутировал и измерял напряжения.
Короче, из той статьи можно срисовать полезные формулы, и прочитать финал статьи…
ну а если не лень, то и всю статью можно прочитать…
Изюмина в том, что лампы можно обсчитывать комбинируя самые различные номиналы с самыми различными типами…
можно соединять автомобильные с осветительными и с фонариком и с гирляндой…в произвольных сочетаниях…
Расчет даст очень приличное соответствие опыту…
формулы можно перерисовать…
https://www.proza.ru/2016/09/22/1863
..
А если хотите могу подготовить статью для вашего сайта…
более подробную и более понятную и развернутую…
На условиях абсолютного бескорыстия – пусть люди пользуются…
улыбнулся.
Станислав, да, конечно!
Буду благодарен и я, и читатели!
Присылайте статью, можно её доработать, количество фото и рисунков – не ограничено)
Пишите мне, см. стр. Контакты.
Александр, давайте так порешим.
Я беру срок до Нового Года…Наверняка я управлюсь и быстрее но…на всякий случай…
Меня единственно что волнует – в формате ВОРД(.doc) вас устроит? Там я скомпоную и рисунки и пояснения как мне это покажется наиболее доходчиво.
Ответьте мне вот на этот вопрос – про формат, чтоб не делать зряшнюю работу…
а когда у меня все будет готово, мы опять ТУТ свяжемся и договоримся как вам передать весь файл…
Можно текст (да, Ворд удобнее) и рисунки отдельно, ничего компоновать и форматировать не нужно. Единственно важно – разбить на разделы (главы) по смыслу и абзацы.
Я всё равно сначала вставляю при верстке текст, а потом файлы рисунков по одному.
Можно по тексту статьи писать “рис.1”, “рис.2”, … А файлы рисунков 1, 2, … выслать отдельно.
Станислав, а Вы не могли бы и мне скинуть этот файл на почту? Желательно .txt с картинками в zip-е? Если можно, конечно…)
Прочитал статьи на proza.ru и меня интересует как теоретически Вы пришли к U^3/P^2? Если можно, подробнее для меня?)
Станислав сейчас готовит расширенную версию статьи, которая будет опубликована на СамЭлектрик.ру.
Как раз там и будут рассмотрены подробно все расчеты, с картинками.
Хорошо я учту пожелания и приведу рассуждение, которое подвело меня к этой зависимости…
Коль скоро я выкладываю материал на бескорыстной основе то и любой сможет скачать отсюда все что его заинтересует.
Готовить материалы в разных форматах мне было бы ЛЕНЬ (признался честно)
Лучше я обстоятельно все распишу а к требуемому формату каждый приведет самостоятельно…
Любой человек думает “собственным образом” и если после опубликования статьи все-таки возникнут вопросы я с удовольствием на них отвечу…
Напоминаю (и не отказываюсь) – срок декабрь)))
Ну, хорошо, уважаемые Александр и Станислав, благодарю за ответы, и да будет так))) Сейчас подпишусь на новости сайта… ;-)
Александр, я подготовил как обещал…
Получился вордовский файл размером 12 страниц…
Формулы я изобразил рисунками.
Сперва попытался их записывать средствами Ворд но потом отказался от этой затеи, ибо любое преобразование файла в (.тхт) деформировало бы текст то полного невосприятия…
я сделал текст и ТАМ ГДЕ ТРЕБУЕТСЯ внедрил РИСУНКИ с формулами…
Рисунков много (ибо формул много) и я в растерянности как их РАЗНОСИТЬ?!
Я упаковал вордовский файл в архив и сформировал еще один архив с шестью фотографиями.
Я там демонстрировал один интересный эксперимент…
Укажите еще раз АДРЕС ПОЧТЫ куда я мог бы “отгрузить” эти два файла…?
архиф фотографий и заархивированный вордовский файл
Отлично, спасибо!
Отправить можно по эл.почте, или через контактную форму, любым удобным способом, см. стр. Контакты.
все…отослал файлы… в колмментарии написал что буду “на страже”…если какие то неясности моментально отреагирую… просьба сразу сообщите распаковалось удачно или возникли проблемы?
если потребуется могу написать “монотонный рассказ” в форме обычного “трепа” на тему как я подкрался к этой идее “расщепления” Закона Ома “вдоль” формулы)))
Статья Станислава опубликована.
Я добавил на основе его формул дополнение к статье.
Вывод – мой практический эксперимент полностью совпадает с формулами Станислава!
Александр, приветствую…
Я ознакомился с вашим дополнением.
Результат совершенно замечательный.
Попробую сформулировать итоги.
Мне приятно, что моя статья явилась для вас нектороым стимулом, чтобы переосмыслить результат, полученный в далеком 2011 году.
\Улыбнулся\
Мгновенно взглянув на ваши таблички особенно на колонку 2 и колонку 4
Я окончательно уверовал в то, что не пропадет “наш скорбный труд и дум высокое стремленье”
\Смеюсь\
Если просто смотреть на колонки 2 и 4, то отчетливо видно, что в колонке 4 я наблюдаю квадратный корень из колонки 2
Вижу “цифирь” 0,25… , мысленно извлекаю квадратный корень и читаю в колонке 4 ОТВЕТ – получится 0,5…
Пронормировав данные к номинальному значению, вы фактически освободились от любой “коэффициентности” и получили ЧИСТУЮ зависимость типа:
У = корень (Х)
И это просто замечательно.
Это ЭКСПЕРИМЕНТАЛЬНО подтверждает мои теоретические соображения, что зависимости тока и сопротивления подчиняется закону степени 1\2 из приложенного напряжения.
Когда я выводил свою главную зависимость (постоянство отношения куба напряжения к квадрату мощности) я первое время долго сомневался.
Сомнения были в стиле – ” а вдруг это просто так совпало для конкретной лампочки” и тому подобные сомнения…
Потом время укрепило мою уверенность, и вот ВЫ совершенно независимо от меня продемонстрировали ЭКСПЕРИМЕНТОМ, что “теория работает”…
Без экспериментального обоснования любая “теория мертва” (как сказал Поэт), а “древо жизни пышно зеленеет”)))
Вот и соединили теорию с жизнью…
Фактически вы своим экспериментом ПОДТВЕРДИЛИ мою теоретическую предпосылку, а теория (в свою очередь) ОБЪЯСНИЛА результаты вашего эксперимента.
Пазл сложился.
Я предлагаю вот что.
Нам надо объединить две статьи как бы “ВОЕДИНО” и подавать на конкурс в виде “сладкой парочки” (два в одном)
Почему так?
А потому что без вашего эксперимента, моя теория “висит в воздухе”.
Можно долго тыкать тестером и проверять всевозможные лампочки и никакое количество проверок НЕ ГАРАНТИРУЕТ, что так будет “всегда”.
А ваша ПРОНОРМИРОВАННАЯ экспериментальная зависимость она будет соблюдаться ДЛЯ ЛЮБОЙ лампочки.
Лично у меня в этом нет никаких сомнений…
Кому не лень, те могут взять ЛЮБУЮ лампочку (другую чем у вас в эксперименте) и я ГАРАНТИРУЮ, что добросовестно проделанный (повторенный) опыт даст те же самые значения в колонках 2 и 4 как и в вашей табличке.
Моя убежденность коренится в том что вы в колонках 2 и 4 получили график вовсе не лампочки (смеюсь), а график алгебраической зависимости :
===> У = корень (Х)
ВОТ В ЧЕМ ДЕЛО!!!
———————
Обдумайте мое предложение, и если вас такой вариант устроит, то мы обсудим как удачнее скомпоновать нам обе статьи…
В любом раскладе я просто вынужден буду сделать ссылку на ваши результаты как на ЭКСПЕРИМЕНТАЛЬНОЕ ОБОСНОВАНИЕ моих соображений…
————-
Ну и … все-таки рекомендую убрать лозунги про “переписывание справочника по физике”)))
там и без наших лампочек много умных и полезных вещей написано)))
Физика наука обширная и клином на лампочках не сошлась)))
Хотя, справедливости ради, наши усилия вполне заслуживают маленькой сноски в справочнике)))
Формула простая и людям будет удобна…
Лично я пользуюсь ей даже в уме.
Я помню, что параметр S для стоваттной лампы на 220 вольт равен 32….
И если мне надо подсоединить ее к автомобильному аккумулятору, я мысленно извлекаю корень из 12…мысленно получаю примерно 3,3…мысленно умножаю на 32 и говорю, что сопротивление будет примерно 100 Ом… ну, а ток примерно 120 миллиАмпер)))
Быстро и удобно)))
===============
ЗЫ. И вот еще что .
Александр, я предлагаю вам пользоваться параметром «S – квадрат»
Так удобнее.
Иными словами, я, когда рассуждаю о постоянстве отношения куба напряжения к квадрату мощности я говорю что эту константу удобнее понимать как квадрат некоей величины …
«S – квадрат»
И далее, пронормируем ток и мощность и получим чистые зависимости:
U = I^2 = R^2;
P^2 = U^3
Равенства будут справедливы также для любой лампы накаливания! Отлично! Освободились от константы!…)))
Ну, и из первого равенства получаем ПРЯМУЮ пропорциональность:
I^2 = R^2
или =>
Iнорм = Rнорм
Упростили, так сказать, лампочку до нельзя…)))
И, Станислав, по-моему теория как раз “не висит в воздухе”, потому как Вы сами уже многократно убедились на практике, что она действует.) А следом Александр и я…
Ну, а нормирование – это ведь чистая алгебра, т.е преобразование УЖЕ ПОЛУЧЕННЫХ формул, из чего следует, что формулы пронормированных тока, сопротивления и мощности будут ТАКЖЕ справедливы)))
А учитывая, что U = I^2 = R^2, получаем для мощности:
P^2 = U^3 = (I^2)^3 = (R^2)^3
=>
P = I^3 = R^3
Вуаля! Т.е. получается нормированная мощность есть кубическая зависимость от тока и сопротивления!
Ну, что ж, прав был Поэт, когда сказал:
“…о, сколько нам открытий чудных, готовит просвещенья дух!…” )))))
Дмитрий, меня искренне радует что вас так увлекла тема лампочек)))
Ваше последнее “алгебраически выведенное” соотношение
P = I^3 = R^3
Можно “получить” ПРОЩЕ)))
В преамбуле к своей статье, в параграфе посвященной “теоретических” аспектов, я написал что-то типа:
“Было сделано предположение что ток и сопротивление имеют единую физическую природу – и то и другое следует считать движением носителей заряда”…
И уже из этой фразы, вспомнив выражение для мощности, можно “без мучений” записать:
Р = I * I * R
значит
P = куб (I) или куб (R)
ну… раз сопротивление и ток – это “одно и то же”, то почему бы и не приравнять…?!…
———-
Но “теория” такая “противная” (смеюсь), что ложка дегтя последовала незамедлительно…
“Теория” УТОЧНЯЕТ, что ток – это упорядоченное движение электронов, а сопротивление – это хаотичное движение.
Грубо говоря, ток – это движение “вдоль провода”, а сопротивление – это движение “поперек провода”…
Улыбнулся.
Ну, а далее надо долго размышлять – ПОЧЕМУ движение “вдоль” не следует отождествлять с движением “поперек”…
Моя версия такова. Потому что движение вагона ВДОЛЬ рельсов и раскачивание вагона в поперечном направлении… все-таки не одно и тоже…
)))
Станислав, действительно, учитывая, что I = R, и ВОВРЕМЯ вспомнив формулу P = I^2*R, можно было сразу так и записать… Но перед моим взором на тот момент маячило полученное “чистое” P^2 = U^3, откуда и был получен ответ.) Как говорится, математика хороша тем, что конечный результат не зависит от выбранного к нему пути – но чем короче путь, тем лучше…)))
И та же математика учитывает и подтверждает теорию, а иненно то, что I и R все таки не “одно и тоже”. Ведь полученное в результате нормирования формулы R = k*I “чистое” равенство Rнорм = Iнорм как раз и означает, что изменение этих величин относительно их номинала и собственно сами величины – это не одно и тоже…)
Тема лампочек меня увлекла давно, Станислав…)) Еще будучи студентом очень занудного) факультета “проектирование и производство РЭА”, я задался целью превратить “лампочку Ильича” в формулы. Мной было снято несколько ВАХ ламп, а так же найдено несколько обобщенных графиков других их основных параметров…
В результате были получены простые формулы наработки на отказ и светового потока (которые я упомянул здесь в комментах статьи “Белые пятна лампы накаливания”)…
К сожалению, до анализа ВАХ и вывода формул электрических зависимостей – дело не дошло – помешала защита диплома, ну а после жизнь-матушка круто “закружила и понесла” и дело было отложено в “долгий ящик” на неопределенный срок…
И когда я прочитал Вашу статью на проза.ру, то был приятно удивлен, что кому-то кроме меня была интересна ЛН в формулах). Кстати, Вы вывели формулы основных эл.зависимостей, но совершенно другим путем чем это собирался сделать я… Так что я искренне рад, что нашел и прочитал Вашу статью! И теперь, благодаря Вам, Станислав, то, что я начал еще студентом наконец завершено! А именно: сложилась “полная картина” основных параметров ЛН!
Вот они, родимые, нормированные зависимости от напряжения:
R = U^0,5
I = U^0,5
P = U^1,5
Ф = U^4 (светов.поток)
n = U^2,5 (светов.отдача)
T = 1/U^13 (наработка на отказ)
Этим моим приближенным формулам тоже можно верить!
Мерить по формуле Ома нельзя она совсем не отражает реальности . Так как не учитывается свойства материала плотность температуру нагрева и так далее в итоге получаем данные по формуле ОМа которые далеки от дейсвительности . Подбор должен быть только методом тыка . Все остальные формулы от лукавого
Грег, формулы не от лукавого, а от науки. Просто ими надо уметь пользоваться и учитывать конкретные условия работы оборудования, вводить соответствующие поправки. А метод тыка существует для проверок.
Тыком проще и не надо заумный формул, А то холодная 20ом, а горячая в 10раз больше.Не впечатлил меня этот ОМ.
Интересно вас почитать, но у меня образования совсем никакого нет.А сопротивление лапочки мне нужно узнать. Измерил мультиметром – не поверил. Получилось 24ом у 200wt лампочки.Потому и полез на ваш сайт, в надежде прояснить истину, т.к. стиралка сломалась и нужно обойти УБЛ замка люка.Ну и понял , что верить теперь ничему нельзя.
Мало того ,что мне выучившему в церкви у дьякона только отче наш, впаривают не только лохотронскую технику, но и приборы такие же.К сожалению из вашей математики я ничего не понял.Вопрос остался открытым.Как узнать сопротивление лампочки?
Спасибо этому дому, пойду поищу где попроще.
Простыми словами, сопротивление лампочки не одинаково, и зависит от напряжения.
При нулевом напряжении сопротивление одно, при 220В – совсем другое, это объясняется законами физики.
Только при чем тут стиральная машина, я не понял?
В стиралке нужно убрать блокировку замка, она работает по принципу чайника. Там нагревательная таблетка,её хочу заменить на резистор.Вот я и подумал заменить лампочкой.Но видно не получится.Теперь я полагаю мне нужно замерить амперы не контактах и высчитать сопротивление ,какое нужно.Ну и искать резистор.Сегодня только узнал , что резисторы ещё и wt определяются.Вот и подумал , что лампа будет лучше, она загорится во всю мочь на крайний случай.Спасибо за внимание.
Я так и сделал. И так мне эта конструкция понравилась.
А тема не раскрыта-фигня ваши лапочки. Вот подключил последовательно трансформатор 220/12 вход через 75 вт R=60 om, выход 12 в.0.5 om -Бздынь!)
Столкнулся с выявленным вами явлением на практике.
Пульт управления парилкой Harvia с сенсорным пультом управления.
Там есть сенсорная кнопка включения света.
6 ламп накаливания 40Вт.
На плате перед выходом на клеммы подключения освещения предохранитель 2,5А.
Изредка предохранитель перегорает по неизвестной причине.
И вот, благодаря вам, причина ясна.
Хотя, замер сопротивления цепи из 6-ти ламп, показывающий 22 Ом должен был вызвать сомнения.
А прикладывая разные напряжения к лампе вы учитывали, что у вас сопротивление источника тока меняется? Знали вы на тот момент о законе Ома для полной цепи? Может надо учебник физики внимательней изучить, а не переписывать?
Алмас, используя блок питания, я предполагал, что это источник напряжения. Соответственно, его внутренним сопротивлением пренебрегал.
У Вас другое мнение?
есть закон Ома для полной цепи. При чем тут мое мнение? Электротехнике как науке 100 лет. Мое мнение – изучение теории требует терпеливости.
Ну как же, сказали “А” – говорите и “Б”.
Мое мнение – внутреннее сопротивление источника напряжения настолько мало по сравнению с сопротивлением лампочки, что им можно пренебречь.
Возможно, у Вас найдется немного терпения, и я всё-таки услышу Ваше мнение?
Кажется, что формула В³ / Вт² = Const излишне усложнена. Применяя соотношения Вт = В * А и Ом = В / А, получаем:
Const = В³ / Вт² = В³ / (В² * А²) = В / А² = (В / А) / А = Ом / А.
То есть, размерность этой константы – Ом на Ампер. И физический смысл в такой формулировке гораздо прозрачнее: Const = Ом / А означает, что Ом = Const * A. Проще говоря, сопротивление лампы накаливания пропорционально току через нее. Вот и вся нехитрая суть этой хитрой формулы :)
Суть этой формулы в изначальном вычислении константы. Зная номинальную мощность лампы и напряжение, на которое она рассчитана, определяется константа. А далее, задавая требуемое сопротивление лампы (или ток, на выбор), можно определить какое напряжение необходимо на неё подать. Просто “Ом = Const * A” на практике работает только если известна константа, которая легче всего считается по исходным (номинальным) значениям.